1.1.1 Kinematics Basics
Kinematics
Definitions
Kinematics is the science of motion. In human movement, it is the study of the
positions, angles, velocities, and accelerations of body segments and joints during
motion.
It's important to define these terms precisely.
Body segments are considered to be rigid bodies for the purposes of describing the
motion of the body. They include the foot, shank (leg), thigh, pelvis, thorax, hand,
forearm, upper-arm and head.
Joints between adjacent segments include the ankle (talocrural plus subtalar
joints), knee, hip, wrist, elbow and shoulder.
Position describes the location of a body segment or joint in space, measured in
metres. A related measure called displacement refers to the position with respect
to a starting position. In two dimensions, the position is given in Cartesian
co-ordinates, with horizontal followed by vertical position.
e.g.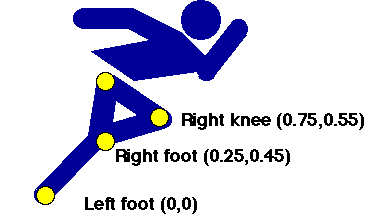
In three dimensions all three directions must be defined:
e.g. (1.5, 6.2, 3.2), (2.8, 9.6, 7.8) etc.
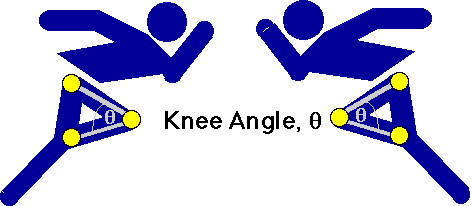
Joint angle (also called inter-segmental angle) is the simply the angle between the
two segments on either side of the joint, usually measured in degrees and often converted
to clinical notation. Since joint angles are relative to the segment angles, they don't
change with the body orientation.
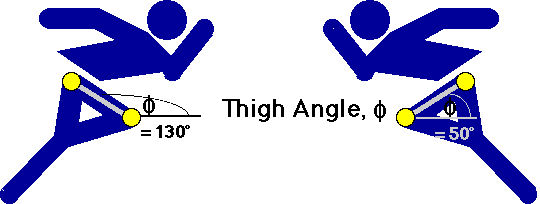
Segment angle is quite different. It is the angle of the segment with respect to
the right-hand horizontal. Note that it is an absolute measure, meaning that it changes
according to the orientation of the body.
Velocity is another word for speed. Velocity may be linear (change in
position) measured in metres per second (m/s or ms-1), or angular (change in
angle), measured in degrees per second (deg./s or deg.s-1). Normally, velocity is derived
from position or angle data by the process of differentiation.
Velocity = distance moved / time taken
Thus if the knee moves from a horizontal position of 1.5 m to a position of 1.6 m in 1/50
of a second, it has a velocity of
Velocity = (1.6 - 1.5) / (1/50)
= 0.1 x 50 = 5 ms-1.
Acceleration is change in velocity. Again, it may be linear (change in
linear velcocity) measured in metres per second per second (m/s2 or ms-2), or angular
(change in angular velocity), measured in degrees per second per second (deg./s2 or
deg.s-2). Acceleration, too, is usually calculated from the position data by
differentiating twice. It can also be measured directly by an instrument called an accelerometer.
Use of kinematic measurements
Kinematic measurements are limited in what they can tell us about the causes of motion
is - for this we need to look at the kinetics. However, they do provide a description
of the motion which can be valuable for certain purposes.
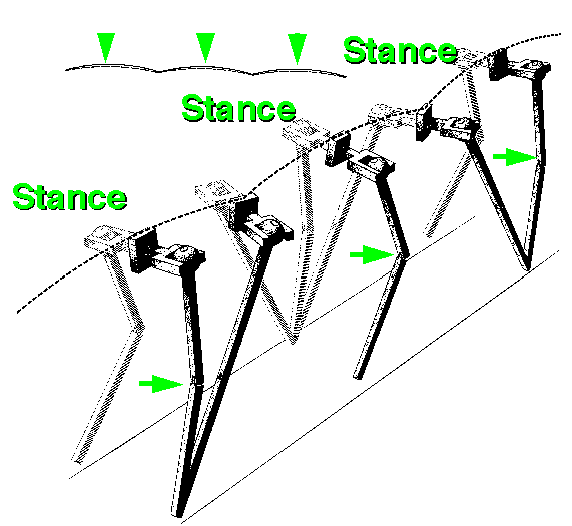
Stance-phase kinematics
One important observation we can make from looking at the kinematics is the amount of
up-down and sideways motion. In actions such as walking and running, the body is
attempting to move horizontally across the ground - any other motion, especially vertical,
does not help this objective, and uses up precious energy.
If the body had wheels it could avoid vertical motion all together, but since we have
legs, there must be some vertical motion. The reason for this is that at heel-strike and
toe-off the two legs make up the sides of a triangle, while during mid-stance the stance
leg is vertical:



Heel-strike -----------------> Mid-stance -----------------> Toe-off
This has the effect of lowering the upper-body (often called the HAT segment for
Head-Arms-Trunk) at heel-strike and toe-off (which together make up the phase known as double
stance, when both feet are in contact with the ground), and raising it during mid-stance:
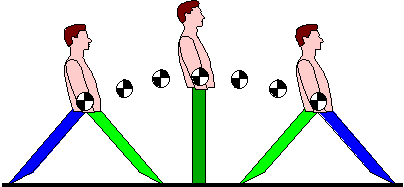
Heel-strike -----------------> Mid-stance -------------> Toe-off
By the way, the funny cross-like sign means the body centre of mass (CoM), which is
located in the HAT segment (in the pelvis). In order for the CoM to rise up between
heel-strike and mid-stance, energy must be expended, which is not gotten back when it
drops back down again at toe-off. This up-down motion of the CoM is therefore inefficient,
and we will see the locomotor system has several methods to try to reduce its amplitude.
The Determinants of Gait
After the second-world war, there were a large number of limbless ex-servicemen in the
United States. The Government realised that a major effort was needed to develop improved
prostheses, particularly lower-limb prostheses, to get these people walking again. As part
of this large research project, the University of Calfornia at Berkely was requested to
perform comprehensive studies on normal and disordered locomotion. Out of this research
came much of our present understanding of the biomechanical mechanisms used in walking and
running.
Several of these key mechanisms relate to the methods used by the body to reduce the
up-down and side-to-side motion of the body CoM, and because of their fundamental
importance to walking biomechanics, they have been called the Determinants of Gait. The
determinants have two main goals: to reduce the maximum height of the body CoM during
mid-stance, and to increase the minimum height of the body CoM at heel-strike and toe-off.
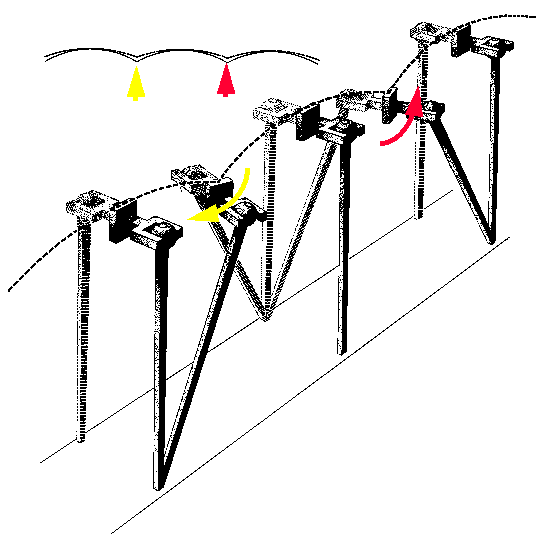
a) Pelvic rotation
The pelvis rotates anteriorly at heel-strie, and posteriorly at toe-off to increase the
effective leg-length at these times:
b) Pelvic list
The pelvis lists downward (obliquity) to increase the effective leg length at toe-off and
heel-strike:
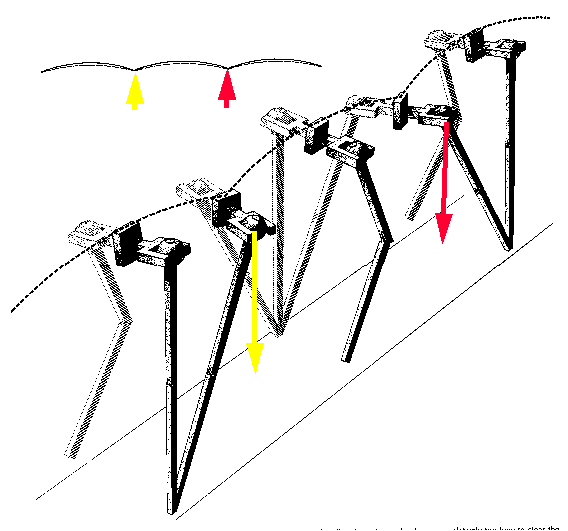
c) Stance Phase knee flexion
A slight flexion of the knee lowers the CoM during stance:
d) Ankle rockers
The ankle is dorsiflexed at heel-strike and plantar-flexed at toe-off. Both these actions
increase the length of the leg(see pictures above).
e) Transverse rotation of leg segments
The lower-limb is lengthened by external rotation, and shorted by internal rotation.
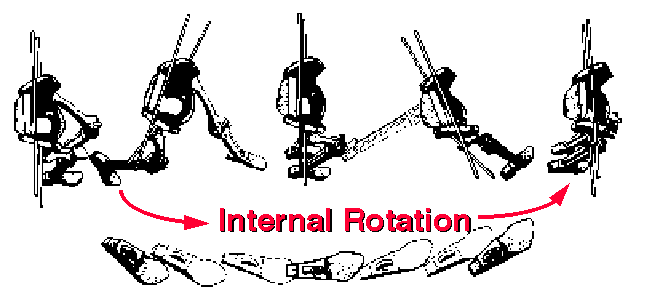

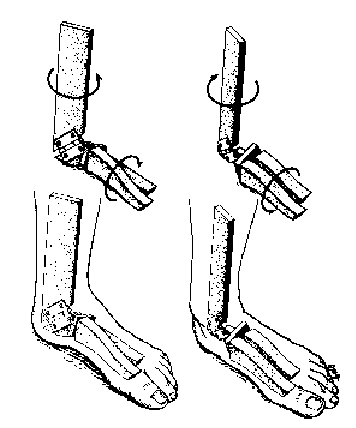
In the foot, these rotations are facilitated by the torque-converter effect,
whereby pronation at heel-strike is converted to internal tibial (and subsequently
femoral) rotation, and external rotation of the femur at toe-off is converted into
supination of the foot. These actions are a consequence of the axes of the talo-crural and
talo-calcaneal (subtalar) joints:
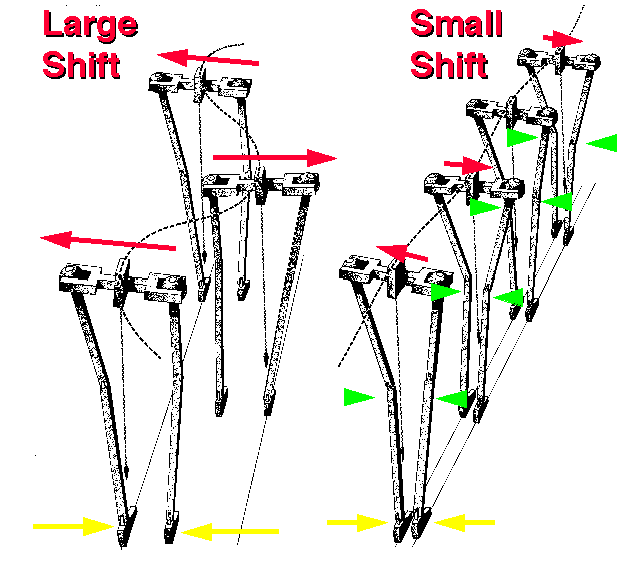
f) Genu valgum The anatomical valgus at the knee permits a narrower walking base,
and thus a smaller lateral shift, than would otherwise be necessary:
All these actions in themselves contribute very small reductions in the amplitude of the
CoM (pelvis) motion, but added together, they reduce it considerably, to around 50 mm
(up-down and side-to-side) in normal gait.
Swing-phase kinematics
An essential prerequisite for gait is to be able to shorten the swing leg
before propelling it foward. The main way this is achieved is by flexion of the knee. This
amount of swing-phase knee-flexion is proportional to the stride length, and thus the gait
velocity (Kirtley et al, 1985):
Many gait pathologies (e.g hemiplegia, diplegia, knee osteoarthrosis) impair swing-phase
knee flexion, causing compensatory mechanisms to be used, such as hip-hiking,
lateral-tilting and circumduction.
Summary of sagittal-plane joint angles
So, basically, you can think of the actions of the knee and ankle joints as
compensating for the flexion-extension motion of the hip. At extreme flexion of the hip
(at heel-strike and toe-off) the knee is extended, while during stance knee flexion and
ankle dorsiflexion help to reduce the effective height of the body.
Other useful kinematic measures
Other useful kinematic measures relate to the risk of falling. In general, there
are two types of fall: the trip, and the skid. The former is a result of the
low foot clearance during mid-swing, typically about 1.5 cm, while the latter is
caused by a high forward velocity at heel-strike. Moreover, it is possible that the
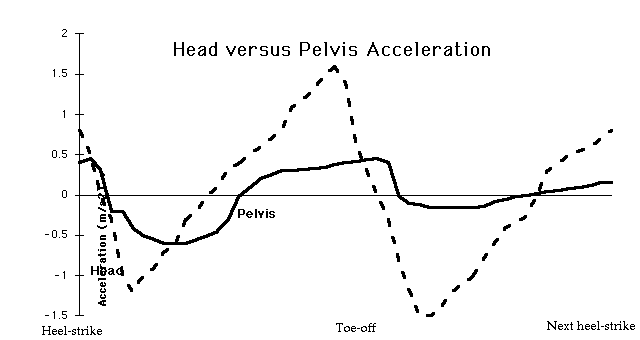
vestibular organ may be disorientated by high accelerations from the lower-limbs if they
are not (as is usually the case) attenuated by the spine. Thus, the head to hip forward
acceleration ratio has been used to gauge the efficiency of this spinal damping
mechanism.
References
Kirtley C, Whittle MW & Jefferson RJ (1985) Influence of Walking Speed on Gait
Parameters Journal of Biomedical Engineering 7(4): 282-8.
Inman & Saunders, Human Walking (2nd Edition).
Winter DA (1991) The biomechanics and motor control of human gait: normal, elderly and
pathological. University of Waterloo press, Ontario.