1.1.2 Kinetics Basics
Forces & Moments
There are two types of force acting on the body:
Load - caused by the acceleration due to gravity (body weight)
Shear - caused by friction between the body and the ground
Load

The unit of force is the Newton (N), named after the English scientist who in 1667
discovered the famous relationship:
Force = mass x acceleration
F = m.a ... (1)
This very important equation tells us that force is proportional to acceleration. Thus the
downwards force on a falling apple due to gravitational acceleration (called g, and equal
to 9.81 m/s2, or approximately 10 m/s2) is:
Force = body mass x acceleration due to gravity
F = m.g
which would be, for example, 0.1 x 10 = 1 N for a typical apple with a mass of 100 grams
(0.1 kg). Newton was said to have discovered the equation when he watched an apple falling
off a tree.
Ground Reaction Force
When a body is not free-falling but in contact with the ground, this force is reflected
back onto the body as a reaction, which is really another word for weight. Thus a
typical apple experiences a reaction of 1 N. When a person stands still, this ground
reaction force is equal to the person's mass multiplied by the gravitational
acceleration (F = m.g). For a typical person of mass 80 kg, this reaction will be (80 x
10) 800 N. Bathroom scales measure this reaction, and the dial should really read in
Newtons, but since gravity is almost constant around the world, they measure mass by
dividing all the readings by 9.81 ms-2. Note that the scales would not be accurate if they
were used on the moon, where gravity is about 1.6 ms-2!
Center of Pressure
This reaction force acts upwards towards the body from all the parts of the body in
contact with the ground (normally the feet). The distribution of this force (pressure)
over the soles of the feet is not even, and more force is taken by some parts of the sole
than others.

When all the forces over every part of the sole are averaged together, the ground reaction
force can be represented by a single force acting a point called the centre of pressure
(CP).
Stand still and try to feel where the centre of pressure is on the soles of your feet.
Is it under the toes? Under your heels? Somewhere else? Is it the same on both sides? Try
to move the centre of pressure under your toes by leaning forward and under your heels by
leaning backwards (this is more tricky!). Then stand normally again and try to feel where
it is.
Question: Why is it more difficult to lean backwards?
The centre of pressure must stay within the foot otherwise the body will topple over. In
fact, the normal position for the centre of pressure during standing is about 5-6 cm in
front of the ankle, or about half-way along the foot from heel to toes. It almost never
goes behind the ankles, because the foot is "L" shaped rather than "T"
shaped - there's a lot of foot in contact with the ground in front of the ankle, but only
a small amount (the heel) behind. This is why you lose your balance when you try to lean
backwards.
Moment of force
The fact that the ground reaction normally acts 5-6 cm in front of the ankle has big
implications. Imagine two people on a see-saw, each of weight m.g Newtons:
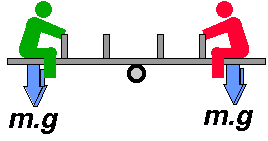
In order to balance the see-saw, the weight of each person (m.g) has to equal. What
happens when one person moves closer to the fulcrum or pivot?
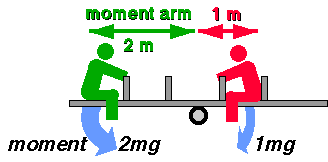
Clearly, the see-saw will tip down at the green end. The reason for this is that the
turning effect of the force is dependant on the distance of the force from the pivot. This
turning effect is called the moment of force (often abbreviated to "moment"),
and the distance is called the moment arm (or lever arm) of the force.
The moment of the force (in units of Newton.metres, Nm) is calculated by multiplying the
force (in Newtons) by the moment arm (in metres).
Ankle moment during standing

Going back to the foot during standing, we can now estimate the moment of force around the
ankle joint due to the ground reaction. We saw that its magnitude was (body mass x
gravitational acceleration, m.g) 800 N for a typical person of mass 80 kg. We also know
that it acts at a point about 5 cm (0.05 m) in front of the ankle joint. Thus, we have:
Moment due to ground reaction = force x moment arm of force
= 800 x 0.05
= 40 Nm
Now, there must be something to balance this moment if the person is standing still,
otherwise the foot would rotate about the ankle. Which way do you think it would rotate?
Remember that the ground reaction acts upwards on the body, and since it's acting on the
sole at a point in front of the ankle joint, it will tend to make the foot rotate upwards
(dorsiflex). What do you think is responsible for balancing the moment due to the ground
reaction to keep the ankle still?
Well, there must be a moment acting in the opposite direction, tending to plantarflex the
foot. Since the ankle is not at the end of its range of motion (so the ligaments are not
stretched) this moment can only come from contraction of the plantarflexor muscles.
In fact, most of this moment is produced by the soleus muscle, which is one of the
strongest and most fatigue-resistant muscles in the body. It has to be, because it has to
produce this moment all the time we're standing, never mind walking or running! You can
get an idea of how big this moment is if you hold a 4 kg mass out at arms length, since
this gives a moment of force of:
Moment = weight x arm's length
= m.g.d
= 4 x 10 x 1
= 40 Nm
i.e. the same as soleus must produce during quiet standing. How does it feel? How long do
you think you could hold the weight in this position?
Inverse Dynamics
The ultimate aim of biomechanical analysis is to know what the muscles are doing: the
timing of their contractions, the amount of force generated (or moment of force about a
joint), and the power of the contraction - whether it is concentric or eccentric.
These quantities can be derived from the kinematics using the laws of physics,
specifically the Newton-Euler
equations:

Newton (linear): F = m.a (Force = mass x linear acceleration)
Euler (angular):
M = I(Alpha) (Moment = mass moment of inertia x angular acceleration)
These equations describe the behavior of a mathematical model of the limb called a link-segment
model, and the process used to derive the joint moments at each joint is known as
inverse dynamics, so-called because we work back from the kinematics to derive
the kinetics responsible for the motion (fig. 1).
This is easily done when the motion is open-chain, with no resistance to motion at
the terminal segment, since all the kinematic variables are known from motion analysis (in
this case Rxd and Ryd of the first segment in the chain, the foot, are both zero). When
there is contact of the limb with another object, such as the ground, or a cycle pedal,
the forces between the limb and the obstructing object in this closed-chain must be
measured. This is usually arranged by the technique of strain-gauging, such as used in a force
platform used to measure the ground reaction force during walking and running.
Such a model is based on several assumptions, e.g.:
that the joints are frictionless pin-joints that the segments are rigid with
mass concentrated at their centers of mass that there is no co-contraction of
agonist and antagonist muscles that air friction is minimal
Whilst these are certainly not always valid for the human body, they are nonetheless
useful approximations in practice for many activities.
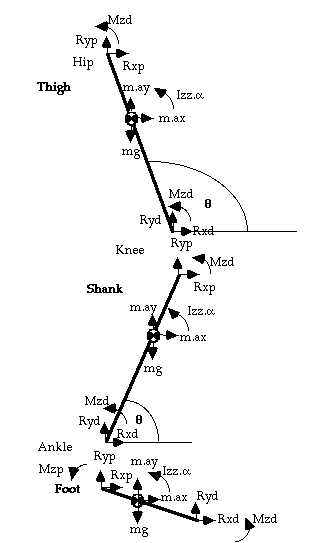
Fig. 1: Link-segment model used for inverse dynamics analysis of the lower-limb
Joint reaction forces
from Newton, Sum of Horizontal Forces, Fx = m.ax:
Rxp = m.ax - Rxd ... (1)
(where p = proximal, d = distal joint, ay = acceleration of segment center of mass, CoM,
in y direction;
Note that d = force platform when p = ankle)
from Newton, Sum of Vertical Forces, Fy = m.ay:
Ryp = m.ay + mg - Ryd ... (2)
Joint moment
about segment CoM:
from Euler, Sum of Moments, Mz = I(Alpha) (where Alpha = angular acceleration)
Mzp = Iz.(Alpha) - Mzd - Rxp.rp.sin(Theta) + Ryp.rp.cos(Theta) + Rxd.rd.sin(Theta) -
Ryd.rd.cos(Theta)
(where rp = distance from segment CoM to proximal joint) (Theta = angle of segment to the
right-hand horizontal)
or, using motion co-ordinates,
Mzp = Iz(Alpha) - Mzd - Rxp.(yp-yCG) + Ryp.(xCG-xp) + Rxd.(yCG-yd) - Ryd.(xd-xCG) ...
(3)
where (xCG, yCG) are the coordinates of the center of gravity of the segment (xp, yp) the
co-ordinates of the proximal joint (xd, yd) the coordinates of the distal joint
It will be noted that several body segment parameters are required to be known,
such as the relative masses and mass moment of inertia (or radius of gyration)
of each segment, the positions of their centers of mass. These are determined mostly from
published cadaver studies, though there now exist automatic techniques for their
estimation in vivo.
Muscle Moment
The moment that we obtain from inverse dynamics tells us which muscle (flexor or
extensor) is active, and how much moment (torque) that muscle is exerting. A common
standard method of representation of these moments in graphical form, a flexor moment
(dorsiflexor at the ankle) is shown as positive, while an extensor (plantarflexor at the
ankle) moment is negative.
For example, the ankle moment curve (fig. 2) indicates a negative (plantarflexor) moment
throughout nearly all of stance, with a very brief and small dorsiflexor moment
immediately after heel-strike. The curve tells us that the main muscle group active at the
ankle throughout stance are the plantarflexors (triceps surae), with steadily increasing
activity through stance up to a maximum just before toe-off, shown in the video picture.
Note that there is a range of values at each time interval - we don't all walk exactly the
same! - the range shows the mean value � 1 standard deviation of a selection of normal
individuals.
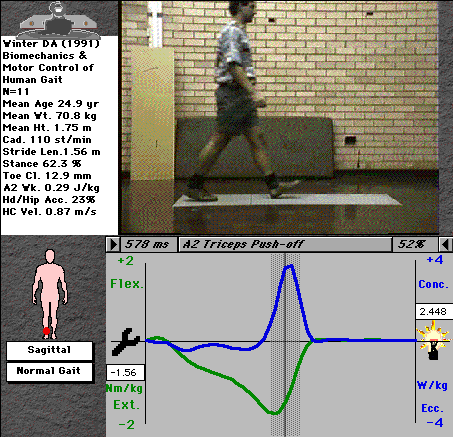
Fig. 2: Ankle moment during normal gait
Mechanical Power
Joint moment thus tells us which muscle (flexor or extensor) is contracting. It does
not tell us why that muscle is contracting. For that we must look at what is termed the
mechanical power. This is the joint moment multiplied by the angular velocity of the
joint. So, if the joint is not moving (an isometric contraction), the angular
velocity, and therefore the power, will be zero. If it is moving in the direction of the
muscle contraction, the power will be positive, corresponding to concentric
contraction of the muscle. If the joint is rotating away from the direction in which the
muscle is pulling, the power will be negative, denoting an eccentric contraction.
This is very useful, because it tells us the function of a muscle contraction: whether the
muscle is being used to do external work, or to absorb energy, in effect to accelerate
or brake the joint.
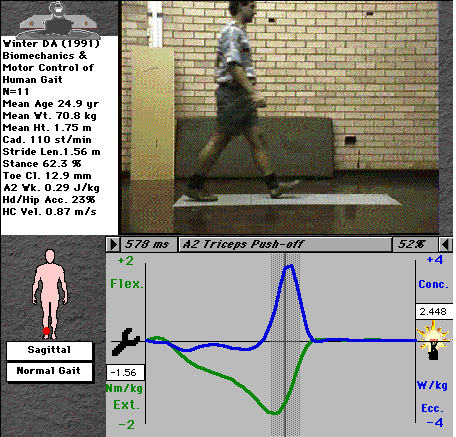
Fig. 3: Mechanical power at the ankle
Joint Activity
The moment and power curves together therefore tell us everything we need to determine
the function of the musculature during a movement. It is sometimes a little difficult to
look at two curves simultaneously, however. A somewhat easier method is to plot the data
instead as a bar graph, with the sign indicating the moment and color (or shading) of the
bars indicating power (fig. 4):
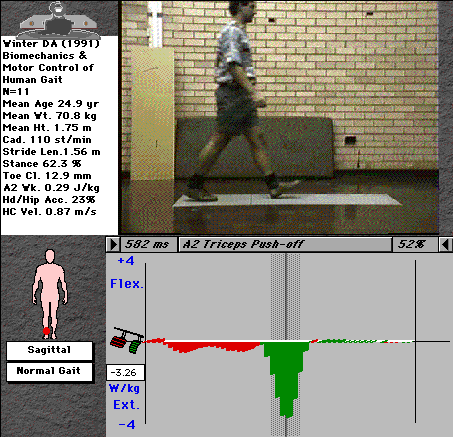
Fig. 4: Ankle joint activity
This chart shows us everything we need to know about the activity of the ankle joint
musculature, clearly indicating the two distinct roles of the plantarflexors during
stance. It also nicely shows the small eccentric contraction of the dorsiflexors (tibialis
anterior and the peronei) immediately after heel-strike to control the foot as it lands,
and their concentric contraction to lift the foot during swing.
Figs. 5 & 6 show the same plot for the knee and hip joints.
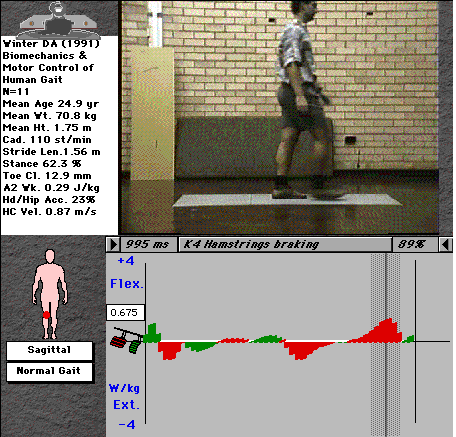
Fig. 5: Activity of the knee-joint musculature (cursor and video shown in K4 phase).
The knee shows 4 phases of distinct activity. K1 is the first eccentric
phase and relates to quadriceps function during the loading response. K2 represents
the same muscle group now acting concentrically to pull the trunk over the stance leg
(about 10-15% of the forward energy of gait). K3 is an eccentric contraction of the
quads to brace the knee against the strong contraction of the triceps (especially
gastrocnemius, which tends to flex the knee as it contracts) at push-off. K4 is
hamstrings braking of the leg during late swing, which increases greatly in running, when
the leg swings forwards much more vigorously (with higher angular velocity).
The hip shows three rather small contractions (though there is considerable variation in
hip function in normal individuals). H1 is a so-called push-from-behind
caused by the gluteus maximus and hamstrings. It may contribute a small amount of forward
energy, but is mainly used to stabilize the trunk at heel-strike. H2 is an
eccentric burst to retard the backwards rotation of the thigh during stance, and H3
is so-called pull-off, coinciding with ankle push-off. H3 is also very much
increased in running.
References
Winter DA (1991) The biomechanics and motor control of human gait: normal, elderly and
pathological. University of Waterloo press, Ontario.
